FÍSICA I - Matutino H1

 

FÍSICA I

La Física siendo parte de las ciencias naturales ha contribuido al desarrolla del ser humano, porque gracias al quehacer científico y a la investigación ha sido posible desentrañar de una forma clara y útil las leyes y principios que rigen el comportamiento de los fenómenos naturales.

 OBJETIVO: Comprender la importancia de la mecánica clásica como motor de los avances tecnológicos para generar satisfactores y beneficios para la sociedad.

EVALUACIÓN

 Para la evaluación de esta materia se recomienda:                                                 

                                                                                30% Tareas*

                                                                                30% Evaluación Final*

                                                                                30% Participaciones en clase

                                                                                10 % Cuestionario

                               §  La asistencia debe ser de un mínimo del  70%, para tener derecho a examen.

§  Se encuentran programadas 5 actividades a realizar.  La calificación final será el promedio de estas actividades; del asesor dependerá los tiempos de entrega de actividades.

 §  Para tener derecho a examen se recomienda el cumplimiento de un mínimo del 70% de las tareas asignadas. 

§  Si el alumno tiene un desempeño completamente satisfactorio, en cuanto a tareas y trabajo en clase, se puede recurrir a la exención de la evaluación final. La calificación será a criterio del profesor.

INICIO CLASE 1 - 4/ABRIL/22

Participación 1

UNIDAD I: LA FÍSICA Y SU APLICACIÓN

INTERPRETAR LOS FENÓMENOS FÍSICOS MEDIANTE LA OBSERVACIÓN Y MEDICIÓN DE LOS MISMOS, ESTABLECIENDO LAS LEYES QUE LOS RIGEN Y SU APLICACIÓN EN LA VIDA COTIDIANA.

 LA FÍSICA

Ciencia que se ocupa de los componentes fundamentales del Universo, de las fuerzas que éstos ejercen entre sí y de los efectos de dichas fuerzas. Sus metas son la comprensión de la naturaleza mediante la elaboración de teorías en base a experimentos.

 CIENCIA Y MÉTODO CIENTÍFICO

 La ciencia suele definirse por la forma de investigar más que por el objeto de investigación, de manera que los procesos científicos son esencialmente iguales en todas las ciencias de la naturaleza; por ello la comunidad científica está de acuerdo en cuanto al lenguaje en que se expresan los problemas científicos, la forma de recoger y analizar datos, el uso de un estilo propio de lógica y la utilización de teorías y modelos.

En el método científico la observación consiste en el estudio de un fenómeno que se produce en sus condiciones naturales. La observación debe ser cuidadosa, exhaustiva y exacta.

A partir de la observación surge el planteamiento del problema que se va a estudiar, lo que lleva a emitir alguna hipótesis o suposición provisional de la que se intenta extraer una consecuencia. Existen ciertas pautas que han demostrado ser de utilidad en el establecimiento de las hipótesis y de los resultados que se basan en ellas; estas pautas son: probar primero las hipótesis más simples, no considerar una hipótesis como totalmente cierta y realizar pruebas experimentales independientes antes de aceptar un único resultado experimental importante.

La experimentación consiste en el estudio de un fenómeno, reproducido generalmente en un laboratorio, en las condiciones particulares de estudio que interesan, eliminando o introduciendo aquellas variables que puedan influir en él.

Una hipótesis confirmada se puede transformar en una ley científica que establezca una relación entre dos o más variables, y al estudiar un conjunto de leyes se pueden hallar algunas regularidades entre ellas que den lugar a unos principios generales con los cuales se constituya una teoría.

Observación Þ Hipótesis Þ Experimentación Þ Teoría Þ Ley

El método científico

RELACIÓN CON OTRAS CIENCIAS

La física está estrechamente relacionada con las demás ciencias naturales, y en cierto modo las engloba a todas.

PRINCIPALES CAMPOS DE LA FÍSICA

	TÉRMINO	DESCRIPCIÓN
	Acústica		Estudia las propiedades del sonido.
	Física atómica		Estudia la estructura y las propiedades del átomo.
	Criogenia		Estudia el comportamiento de la materia a temperaturas extremadamente bajas.
	Electromagnetismo		Estudia los campos eléctrico y magnético, y las cargas eléctricas que los generan.
	Física de partículas		Se dedica a la investigación de las partículas elementales.
	Dinámica de fluidos		Examina el comportamiento de los líquidos y gases en movimiento.
	Geofísica		Aplicación de la física al estudio de la Tierra. Incluye los campos de la hidrología, la meteorología, la oceanografía, la sismología y la vulcanología.
	Física matemática		Estudia las matemáticas en relación con los fenómenos naturales.
	Mecánica		Estudia el movimiento de los objetos materiales sometidos a la acción de fuerzas.
	Física molecular		Estudia las propiedades y estructura de las moléculas.
	Física nuclear		Analiza las propiedades y estructura del núcleo atómico, las reacciones nucleares y su aplicación.
	Óptica		Estudia la propagación y el comportamiento de la luz.
	Física del plasma		Estudia el comportamiento de los gases altamente ionizados (con carga eléctrica).
	Física cuántica		Estudia el comportamiento de sistemas extremadamente pequeños y la cuantización de la energía.
	Física de la materia condensada		Estudia las propiedades físicas de los sólidos y los líquidos.
	Mecánica estadística		Aplica principios estadísticos para predecir y describir el comportamiento de sistemas compuestos de múltiples partículas.
	Termodinámica		Estudia el calor y la conversión de la energía de una forma a otra.

Tarea 1

MEDIDAS FUNDAMENTALES

Sistema Internacional de unidades, nombre adoptado por la XI Conferencia General de Pesos y Medidas (celebrada en París en 1960) para un sistema universal, unificado y coherente de unidades de medida, basado en el sistema mks (metro-kilogramo-segundo). Este sistema se conoce como SI, iniciales de Sistema Internacional. En la conferencia de 1960 se definieron los patrones para seis unidades fundamentales y dos unidades complementarias.

 Longitud

El metro (m) se definió originalmente como una diezmillonésima parte de la distancia entre el ecuador y el polo norte a lo largo del meridiano de París.

 Masa

Cuando se creó el sistema métrico decimal el kilogramo se definió como la masa de 1 decímetro cúbico de agua pura a la temperatura en que alcanza su máxima densidad (4,0 °C).

 Tiempo

Durante siglos el tiempo se ha venido midiendo en todo el mundo a partir de la rotación de la Tierra. El segundo, la unidad de tiempo, se definió en un principio como 1/86.400 del día solar medio, que es el tiempo de una rotación completa de la Tierra sobre su eje en relación al Sol.

Tabla 1-b  UNIDADES BÁSICAS
	Magnitud	Nombre de la unidad  SI básica	Símbolo
	Longitud	metro	m
	Masa	kilogramo	kg
	Tiempo	segundo	s
	Intensidad de corriente eléctrica	amperio	A
	Temperatura termodinámica	kelvin	K
	Cantidad de sustancia	mol	mol
	Intensidad luminosa	candela	cd

 SISTEMA INGLÉS

Algunas medidas del sistema inglés son comunes en nuestro medio, las principales son:

Pulgada               1 pulg = 2.54 cm                          Libra             1 lb  =  454 gr

Pie                        1 pie = 12 pulg = 30.48 cm         Onza             1 Oz = 1/16 lb = 28.7 gr

Yarda                    1 yd  = 3 pies = 91.44 cm           Galón           1 Gal = 3.785 litros

Milla                      1 mi    = 1760 yd = 1609 m

CONVERSIÓN DE UNIDADES

En ocasiones es necesario convertir unidades de un sistema a otro, por lo que se usan las equivalencias entre ellos.

Ejemplo 1.10: Convertir 80 pulgadas a centímetros.

Solución:    80 pulg × 2.54 cm = 203.2 cm

                                 1 pulg

 Ejemplo 1.11: Convertir 80 centímetros a pulgadas.

Solución:    80 cm × _1 pulg_= 31.49 pulg

                                2.54 cm

 Ejemplo 1.12: Convertir 120 kilómetros por hora a metros por segundo.

Solución:   120 km/hr × __1 hr__  ×  1000 m   =  120 × 1000 = 33.33 m/seg

                                       3600 seg       1 km          3600

Realizar las siguientes conversiones:

a) 1000 metros a millas	b) 200 kilogramos a libras
c) 350 pulgadas a metros	d) 1.12 millas a centímetros
e) 1 metro2 a centimetros2	f) 150 km/hr a m/seg.
g) 235 millas/hr a km/hr	h) 1.25 cm a metros.
i) 10 km/hr a cm/seg	j) 1 m/seg a km/hr

FIN CLASE 1 - 4/ABRIL/22

INICIO CLASE 2 - 6/ABRIL/22

Participación 2

EMPEZAR DE COPIAR DESDE AQUÍ

 UN REPASO DE MATEMÁTICAS

 Despeje de ecuaciones

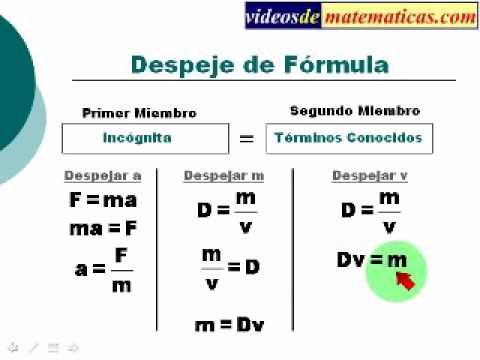
Para despejar una variable en una ecuación lineal se sigue el siguiente procedimiento:

1)    Se reúnen los términos con la variable a despejar en alguno de los lados de la ecuación (lado izquierdo).

2)    Se simplifican los términos.

3)    El resultado es una ecuación de la forma  ax = b, cuya solución es  

4)    Ejemplo 1.1: De la ecuación F = ma, despejar m.

 

Solución: Invirtiendo la ecuación        ma = F

                De acuerdo al paso 3             m = F/a   donde la m ya está despejada.

Ejemplo 1.2: De la ecuación  d = V₀ – ½ at²  despejar a.

Solución: Invirtiendo la ecuación                                        V₀ – ½ at² = d 

               Restando V₀  en ambos lados de la ecuación             - ½ at² = d – V₀

              Cambiando de signo a toda la ec.                                 ½ at² = V₀ - d

             Multiplicando por 2 para eliminar el ½                            at² = 2(V₀ – d)

             De acuerdo al paso 3                                                      

                                                                                                            Donde la a ya ha sido despejada.

 Ejemplo 1.3: De la ecuación   d = ½ at², despejar t

 

Solución: Invirtiendo la ecuación          ½ at² = d

                Multiplicando por 2                 at² = 2d

                De acuerdo al paso 3                 t² = 

                La operación inversa de elevar al cuadrado es la raíz cuadrado, por lo que:

                                                                    t = 

NOTACIÓN CIENTÍFICA

 Los científicos trabajan frecuentemente con números muy grandes y muy pequeños. Por ejemplo, la masa de la Tierra es de alrededor de 6 000 000 000 000 000 000 000 000 kg, y la masa de un electrón es 0.000 000 000 000 000 000 000 000 000 000 911 kg. En esta forma, las cifras ocupan mucho espacio y son difíciles de usar en cálculos. Para trabajar con ellas sin tantas dificultades, pueden agruparse en una notación más corta, expresando los lugares decimales como potencias de 10. Este método de expresar números se llama notación científica.

El punto decimal puede variar de posición, pero el exponente variara de acuerdo a las posiciones del punto, ejemplo:

                       8.34 ´ 10⁷ = 83.4 ´ 10⁶ =  834 ´ 10⁵ = 83400 ´ 10³

                       5.1 ´ 10¹ = .51 ´ 10² = .051 ´ 10³ = .0051 ´ 10⁴

                       5.1 ´ 10² =  51 ´ 10¹ = 510 ´ 10⁰ = 510 = 5100 ´ 10^-1 = 51000 ´ 10^-2  

 

SUMA Y RESTA

Para sumar o restar este tipo de números es necesario igualar los exponentes.

 

Ejemplo 1.4:                  2.4 ´ 10 ³ + 3.2 ´ 10³ =  (2.4 + 3.2) ´ 10³ = 5.6 ´ 10³

                                 3.2 ´ 10¹² – 7.4 ´ 10¹⁰ = 320 ´ 10¹⁰ – 7.4 ´ 10¹⁰ = 312.6 ´ 10¹⁰ = 3.126 ´ 10¹²

Otro método              3.2 ´ 10¹² – 7.4 ´ 10¹⁰ = 3.2 ´ 10¹² - .074 ´ 10¹² = 3.126 ´ 10¹²

MULTIPLICACIÓN Y DIVISIÓN

Los números expresados en notación científica se pueden multiplicar aún cuando los exponentes no sean iguales. Primero multiplique los números que anteceden las potencias de 10. Después, sume algebraicamente los exponentes, reestructurando la respuesta.

 

Ejemplo 1.5:                  (2.4 ´ 10⁶)(4.6 ´ 10⁸) = (2.4)(4.6) ´ 10⁶⁺⁸ =  11.04 ´ 10¹⁴ = 1.104 ´ 10¹⁵

                                   (5 ´ 10²¹)(3.2 ´ 10^-15) = 16 ´ 10⁶ = 1.6 ´ 10⁷

                                   (8.125 ´ 10¹⁴)(5.2 ´ 10^-24) = 42.25 ´ 10^-10 = 4.225 ´ 10^-9

 La división de este tipo de números es de forma similar, pero en lugar de multiplicar es dividir y en lugar de sumar es restar, reestructurando el resultado.

 TERMINAR DE COPIAR DESDE AQUÍ

Ejercicios a resolver:

TAREA 2

Realizar despejes

Realizar despejes

FIN CLASE 2 - 6/ABRIL/22

INICIO CLASE 3 - 18/ABRIL/22

PARTICIPACIÓN 3

Repaso Teorema de Pitágoras

FUNCIONES TRIGONOMÉTRICAS

EJEMPLO DE FUNCIONES TRIGONOMÉTRICAS

TAREA 3

FIN CLASE 3 - 18/ABRIL/22

INICIO CLASE 4 - 20/ABRIL/22

 

Participación 4

Realizar las graficas y cálculos correspondientes, a los ejercicios explicados anteriormente, Ejemplo 2.2, 2.3 y 2.4, en la libreta de apuntes.

Tarea 4

Resolver los siguientes ejemplos, de repaso y copiarlos a la libreta de apuntes.

Ejemplos Resueltos

Suma de Vectores con Gráfica

Suma de Vectores con Gráfica 1

Suma de Vectores con Gráfica 2

Suma de Vectores con Gráfica 3

FIN CLASE 4 - 20/ABRIL/22

INICIO CLASE 5 - 25/ABRIL/22

Participación 5

Vídeos Ejemplos Resueltos

Vectores Introducción

Representación Gráfica con Vectores

Suma de Vectores con Gráfica

Suma de Vectores con Gráfica 1

Suma de Vectores con Gráfica 2

Suma de Vectores con Gráfica 3

Componentes Rectangulares con Vectores

Tarea 5

Introducción Vectores

Ejercicios con Vectores

Descomposición de Vectores

FIN CLASE 5 - 25/ABRIL/22

INICIO CLASE 6 - 27/ABRIL/22

Gráfica deVectores 1

Gráfica de Vectores 2

Participación 6

Tarea 6

FIN CLASE 6 - 27/ABRIL/22

INICIO CLASE 7 - 2/MAYO/22

Participación 7

Suma de Vectores

Tarea 7

En Classroom

FIN CLASE 7 - 2/MAYO/22

INICIO CLASE 8 - 4/MAYO/22

Participación 8

Resolver los siguientes ejercicios.

1.- V=(Vf-Vi) / d² despejar la variable “d”

2.- Notación científica, resolver:

a) 1.6X10² - .2X10³ =

b) 0.95X10-² + (1.9X10-¹) =

c) (18.6X10-³) (9.5X10-¹) =

d) .4X10² / 5X10 =

3.- Realizar las siguientes conversiones: a) Convertir 122 cm en pulgadas y b) Convertir 3m² a cm²

4.- Un avión recorre 35 km al norte, después 50 km dirección 35º al sur del este y al final recorre 20 km 

al sur hallar la distancia y el ángulo de ubicación. (graficar)

5.- Trazar el triángulo rectángulo, anotando los datos e indicando con una letra, el lado que se desea 

calcular. Resolver, para todas las incógnitas, hallar a=?, ϴ=?, β=?, si b=2m y c= 400cm.

6.- Convertir 156 millas/hrs a km/hrs.

7.- Si un objeto se desplaza 7.5 km hacia el este y luego 4.5 km hacia el norte. Calcula su 

desplazamiento neto o resultante. (graficar)

Tarea 8

Resolver los siguientes ejercicios.

1.- d=(at²) / 2 despejar la variable “a”

2.- Notación científica, resolver:

a) .6X10³ + 1.8X10² =

b) (95X10-²) - (5X10-³) =

c) (9X10-³) (18X10-²) =

d) 1.4X10 / 2X10² =

3.- Realizar las siguientes conversiones: a) Convertir 111 cm en pulgadas y b) Convertir 2m² a cm²

4.- Un avión recorre 55 km al norte, después 50 km dirección 25º al sur del este y al final recorre 30 km 

al sur hallar la distancia y el ángulo de ubicación. (Graficar)

5.- Trazar el triángulo rectángulo, anotando los datos e indicando con una letra, el lado que se desea 

calcular. Resolver, para todas las incógnitas, hallar a=?, α=?, β=?, si a=3m y c= 500cm.

6.- Convertir 111 millas/hrs a km/hrs.

7.- Si un objeto se desplaza 4.5 km hacia el este y luego 6.5 km hacia el norte. Calcula su 

desplazamiento neto o resultante. (Graficar)

FIN CLASE 8 - 4/MAYO/22

INICIO CLASE 9 - 9/MAYO/22

Participación 9

Resolver los siguientes ejercicios.

1.- d=(at²) / 2 despejar la variable “t”

2.- Notación científica, resolver:

a) .9X10 + 1.8X10² =

b) (450X10-³) - (50X10-²) =

c) (.5X10-²) (8X10-²) =

d) 1.0X10-² / 2X10² =

3.- Realizar las siguientes conversiones: a) Convertir 100 cm en pulgadas y b) Convertir 1m² a cm²

4.- Un avión recorre 40 km al norte, después 60 km dirección 25º al sur del este y al final recorre 10 km 

al sur hallar la distancia y el ángulo de ubicación. (Graficar)

5.- Trazar el triángulo rectángulo, anotando los datos e indicando con una letra, el lado que se desea 

calcular. Resolver, para todas las incógnitas, hallar a=?, α=?, β=?, si a=4m y c= 700cm.

6.- Convertir 50 millas/hrs a km/hrs.

7.- Si un objeto se desplaza 5.5 km hacia el este y luego 5.5 km hacia el norte. Calcula su 

desplazamiento neto o resultante. (Graficar)

Tarea 9

Resolver los siguientes ejercicios.

Realizar las siguientes conversiones:

a) 500 metros a millas	b) 100 kilogramos a libras
c) 250 pulgadas a metros	d) 0.8 millas a centímetros
e) .50 metros2 a centimetros2	f) 80 km/hr a m/seg.
g) 50 millas/hr a km/hr	h) 50.50 cm a metros.
i) 30 km/hr a cm/seg	j) 5 m/seg a km/hr

1.- A= ( b * h ) / 2 despejar la variable “h”

2.- Notación científica, resolver:

a) .5X10² + 1.0X10 =

b) (45X10-³) - (.50X10-³) =

c) (.5X10-²) (5X10-³) =

d) .4X10-² / 8X10-³ =

3.- Realizar las siguientes conversiones: a) Convertir 35 cm en pulgadas y b) Convertir 1m² a cm²

4.- Un avión recorre 20 km al norte, después 70 km dirección 25º al sur del este y al final recorre 20 km 

al sur hallar la distancia y el ángulo de ubicación. (Graficar)

5.- Trazar el triángulo rectángulo, anotando los datos e indicando con una letra, el lado que se desea 

calcular. Resolver, para todas las incógnitas, hallar a=?, α=?, β=?, si a=4m y c= 6000mm.

6.- Convertir 40 millas/hrs a km/hrs.

7.- Si un objeto se desplaza 6.5 km hacia el este y luego 7.5 km hacia el norte. Calcula su 

desplazamiento neto o resultante. (Graficar)

FIN CLASE 9 - 9/MAYO/22