MATEMÁTICAS IV
maestromemo@gadi.edu.mx
FUNDAMENTACIÓN
La asignatura Matemáticas IV aborda el estudio de la Geometría Analítica, porque estos conocimientos serán básicos para el desarrollo del Cálculo Diferencial e Integral. La importancia de esta asignatura radica en convertirse en herramienta importante y necesaria en la resolución de problemas y, que además junto con la Aritmética, constituya el fundamento teórico-metodológico para las asignaturas posteriores, ya que se han establecido como contenidos integrales, esto es, desde el primer hasta el sexto semestre, y siguiendo el mismo orden, la enseñanza de la Aritmética, Geometría y Trigonometría, Geometría Analítica y Cálculo.
El estudio de Matemáticas IV permite una visualización geométrica de los fenómenos que se presentan en su entorno, así como, su interpretación por medio de la construcción de modelos matemáticos. Por ello, el programa aborda el estudio de la Geometría y la Trigonometría, las cuales permitirán la representación y estudio de los fenómenos físicos, químicos y biológicos y, donde el manejo del Álgebra y la Geometría Euclidiana constituyen el fundamento teórico metodológico.
OBJETIVO: Resolver problemas teórico-prácticos, a partir de las ecuaciones: ordinaria y general de la Recta y Circunferencia, y de las ecuaciones ordinarias de la Parábola y Elipse.
EVALUACIÓN
La evaluación de esta materia será:
30% Tareas
35% Participaciones en clase
10% Cuestionario
25% Evaluación Final
INICIO CLASE 1 - 27/JULIO/24
UNIDAD I: INTRODUCCIÓN A LA GEOMETRÍA ANALÍTICA
GEOMETRÍA ANALÍTICA
Rama de la geometría en la que las líneas rectas, las curvas y las figuras geométricas se representan mediante expresiones algebraicas y numéricas usando un conjunto de ejes y coordenadas.
La Geometría Analítica
La Geometría Analítica que, como sabemos, conecta los conceptos de la geometría con los del álgebra y viceversa; al decir de Descartes, la expresión de curvas por medio de relaciones algebraicas. Ya desde la Antigüedad esta vinculación se trató de plantear. Por ejemplo Menecmo, quien fue discípulo de Eudoxo, se supone que conocía algo de geometría analítica; aunque con las limitaciones impuestas al álgebra por los griegos es difícil que esto haya sido muy desarrollado. Sin embargo, Apolonio de Perga en su famosa obra Las Cónicas, y quien vivió alrededor de los años 262 y 190 a.C., usó rectas de referencia para puntos, también un diámetro y una tangente a la misma para expresar esos puntos; es decir, algo parecido a lo que en geometría analítica moderna hacemos cuando usamos los ejes de coordenadas. También Pappus y Omar Khayyam los usaron en su resolución de ecuaciones cúbicas.
Parte de la obra de Las Cónicas fue traducida por los árabes y fue introducida en Europa precisamente por Edmund Halley (1556-1742) quien fue un científico amigo de Newton.
Muchos otros matemáticos hicieron algunos avances en esta relación entre álgebra y geometría durante esta época. Giovani di Casoli, Nicole Oresme (c. 1323-1382) y el mismo Galileo habían tratado de establecer representaciones gráficas de conceptos como los de tiempo, rapidez, distancia y velocidad; sin embargo, fue René Descartes quien dió el impulso definitivo en esta dirección a la geometría. Subrayemos que Descartes es considerado el primer filósofo moderno y, por eso mismo, debe interpretarse que la geometría analítica corresponde al espíritu de lo que ya es una nueva era en el desarrollo de la sociedad occidental.
La obra de Descartes es auténticamente revolucionaria. Podemos decir que el método que él proponía se reduce a tres pasos:
1- La expresión de un problema geométrico en forma algebraica.
2- Resolución de las ecuaciones algebraicas que corresponden al problema geométrico.
3- Construir o interpretar geométricamente lo que planteaba la solución.
Descartes se dice que buscaba liberar a la geometría del exceso de figuras, pero también buscaba darle sentido o significado al álgebra por medio de la geometría. Fue revolucionario René Descartes
Descartes al establecer que una curva se construye con solamente ofrecer una ecuación algebraica. Recordemos que en la Antigüedad para que una curva existiera era necesario que hubiera un procedimiento con regla y compás para poderla construir.
Fermat. Se le atribuye también la creación de la geometría analítica a Pierre de Fermat, quien escribió sobre estos temas antes incluso que Descartes hubiera publicado su obra seminal sobre el tema, pero que, desafortunadamente, fue publicada de manera póstuma posteriormente a la obra de Descartes.
El Álgebra
Lo importante a subrayar acá es el uso de los métodos algebraicos. Podríamos decir que hasta el siglo XVII el álgebra estuvo subordinada a la geometría y a partir de este momento el rol se invirtió y, con ello, se dio un cambio sustancial en la historia de las matemáticas.
SISTEMA DE COORDENADAS RECTANGULARES
Está formado por dos rectas numéricas perpendiculares entre sí, el eje horizontal llamado eje de las abscisas o eje x. El eje vertical llamado eje de las ordenadas o eje y. En el plano se pueden graficar cualquier punto P con coordenadas P(x,y).
PARTICIPACIÓN 1 - INICIAR A COPIAR, EJEMPLOS DESDE AQUÍ

Eje yEje Vertical
Eje Horixzontal -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 Eje x
Así las coordenadas de los puntos A, B, C, D, E y F son respectivamente: A (-6,3), B (5,4), C (3,0), D (- 4,-2), E (5,-4) y F (0,-6).

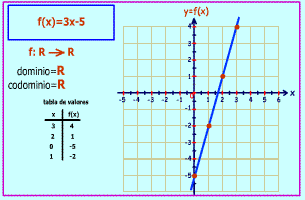
DISTANCIA ENTRE DOS PUNTOS


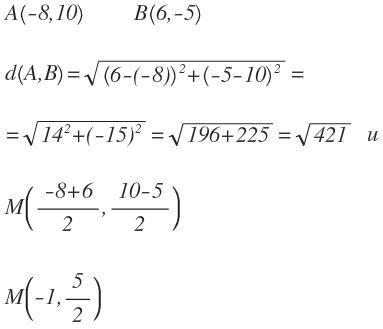
PARTICIPACIÓN 1 - TERMINAR DE COPIAR, EJEMPLOS DESDE AQUÍ
TAREA 1 - EN CLASSROOM
FIN CLASFIN CLASE 1 - 27/JULIO/24
TAREA 1a
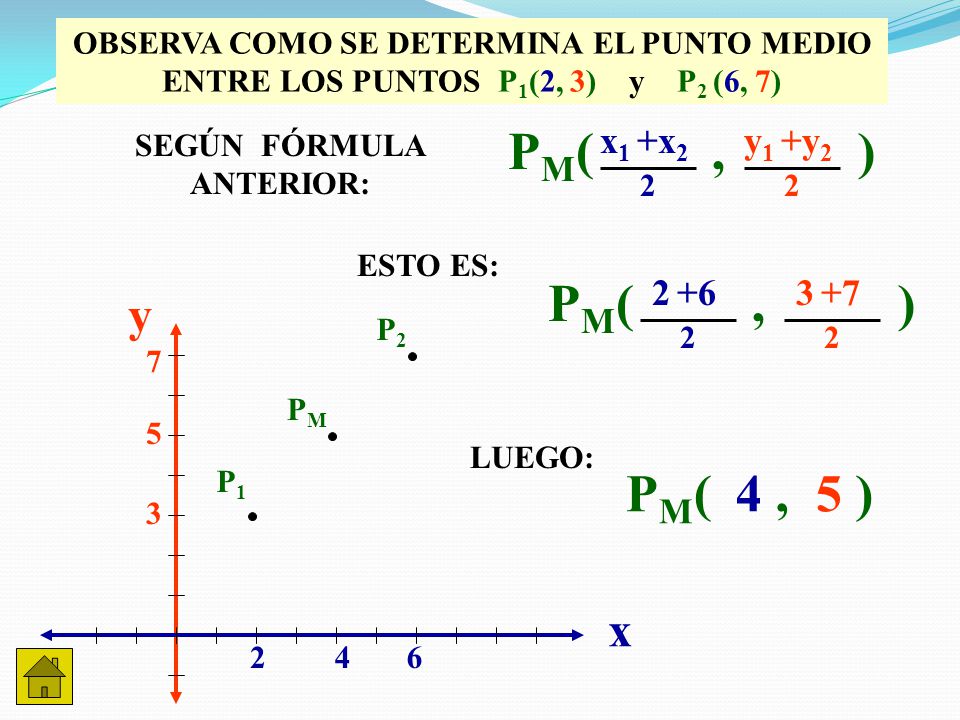
EJEMPLOS - PUNTO MEDIO
INICIO CLASE 2 - 3/AGOSTO/24
PARTICIPACIÓN 2 - INICIAR DE COPIAR, EJEMPLOS DESDE AQUÍ
Ver los videos y copiarlos a la libreta de apuntes.
FUNCIONES TRIGONOMÉTRICAS
EJEMPLO DE FUNCIONES TRIGONOMÉTRICAS
PARTICIPACIÓN 1 - TERMINAR DE COPIAR, EJEMPLOS DESDE AQUÍ
TAREA 2
FIN CLASE 2 - 3/AGOSTO/24
INICIO CLASE 3 - 10/AGOSTO/24
En Classroom.
FIN CLASE 3 - 10/AGOSTO/24
INICIO CLASE 4 - 17/AGOSTO/24
En Classroom.
FIN CLASE 4 - 17/AGOSTO/24







Comentarios
Publicar un comentario