PROPEDÉUTICO DE MATEMÁTICAS

"BIENVENIDOS"

PROPEDÉUTICO DE MATEMÁTICAS

maestromemo@gadi.edu.mx

EVALUACIÓN
Para la evaluación de esta materia:

30% Tareas

35% Participaciones en Clase

10% Cuestionario

25% Evaluación Final

Nota: Cumplir con el 80% de asistencia, para acreditar la materia.

Realizar portada, anotando los porcentajes de evaluación.

OBJETIVOS:

La aritmética fundamental de las matemáticas en base a operaciones fundamentales que son: Adición, Sustracción, Multiplicación, División, Potenciación y Radicación.

El programa del curso comprenderá al desarrollo de habilidades matemáticas a través de una serie de actividades que fortalecen y amplían oportunidades del estudiante, promoviendo el desarrollo de procesos en operaciones matemáticas y así para identificar, analizar, generalizar, representar, modelar y resolver problemas de la cotidianos, aplicado la leyes de los signos.

El curso proveerá de los elementos básicos necesarios para su formación en nivel bachiller, ser individual y social.

Inicio Clase 1 - 22/Agosto/2024

LOS NÚMEROS REALES

La Recta numérica

Números enteros: Conjunto, definición y representación. Paso a paso.

NÚMEROS ENTEROS EN LA RECTA NUMÉRICA
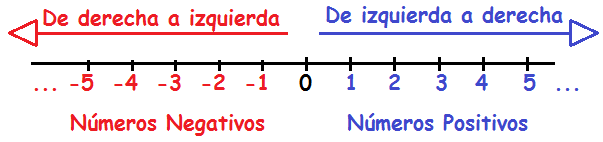
Conjunto ordenado de números que se escribe de forma ordenada sobre una línea horizontal, con marcas a igual distancia, en donde se anotan los números.
Hacia la derecha del cero, se colocan los números positivos y hacia la izquierda del cero, los negativos.

D´ Repaso Virtual: NÚMEROS REALES

Trazamos la recta L y elegimos un punto sobre ella como origen o cero, tomamos un segmento arbitrario como unidad (U).

Relación de orden

La serie de los números naturales está ordenada de menor a mayor. Así, al ver una serie de números ordenados, podemos saber que los anteriores a un número son menores y los que están ordenados después, son mayores que ese número.

Ejemplo:
1 2 3 4 5 6 7 8 9 10
Sabemos que los números que están antes del 6, son menores a éste (1,2,3,4, y 5) y que los que están colocados después, son mayores, incluso aunque no estén escritos. (Por ejemplo el 25 es mayor que 6)

Números Reales

Los primeros números que aparecieron históricamente fueron los números naturales, utilizados para contar. medir, pérdidas y ganancias y profundidades requerimos el 0 y los números enteros negativos, que junto con los naturales forman el conjunto de los enteros.

En mediciones más precisas se utilizan otro números como los racionales e irracionales que en conjunto forman a los números reales.

NÚMEROS NATURALES._ Son aquellos números que utilizamos para contar.

N = {1,2,3,4,5,6,7,8,9,10,11,…}

NÚMEROS ENTEROS._ Tienen parte decimal nulo.

E = {…-4,-3,-2,-1, 0, 1, 2, 3, 4,5…}

NÚMEROS RACIONALES._ Se pueden expresar como la división de dos enteros.

D = {x/x = a ÷ b; a, b Î E, a ≠ 0}

Algunos elementos de D son:

D = {3/4, -8/5, -6, 0, 1.43, -2.454545…, 2938/34089…}

Entre los números racionales se incluyen:

Todos los enteros positivos y negativos. Ejemplo: 4, -7, 0, 345, etc.

Toda fracción (formada por enteros). Ejemplo: 3/5, 187/456,

Todo número decimal finito. Ejemplo: 3.657, -.2934, 35.39475…

Todo número decimal infinito periódico. Ejemplo: 2.3333…,4.363636…, 0.384384384…, etc.

NUMEROS IRRACIONALES._ No se pueden escribir como la división de dos enteros.

Algunos números irracionales son:

Q = { p, e, √2, √3, √5….}

Contiene a los números con raíces no exactas.

NÚMEROS REALES._ Contiene tanto a los números racionales como a los números irracionales.

Algunos números reales son:

R = {3,-5, 0,3/5,-9/37,p, √7, 1.43,3.656565…, etc.}

REGLA DE SIGNOS PARA SUMA Y RESTA

REGLA DE SIGNOS PARA SUMAR O RESTAR

con

+ Se suman y se deja el mismo signo

con

- Se suman y se dejan el mismo signo

con

Se deja el Signo de mayor valor numérico

con

Se deja el signo de mayor valor numérico

SUMA Y RESTA DE REALES

Ejemplos aplicando las reglas de los signos:

1. En suma de números con signos iguales, se suman los números y el resultado lleva el mismo signo. Si los números tienen signos diferentes, se restan y el resultado lleva el signo del mayor.

Ejemplo: 5 + 8 = 13 5 + -8 = -3

2. En resta de signos iguales el resultado lleva el signo del mayor. Si se restan signos diferentes, se suman los números y el resultado lleva el signo del mayor.

Ejemplo: 5 - 8 = -3 5 - (-8) = 13

3. En multiplicación y división de números con signos iguales el resultado es positivo. Si los números son signos opuestos, el resultado es negativo.

Ejemplo: 5 x 8 = 40 5 x -8 = -40

En esta sección aprenderemos cómo realizar las operaciones entre números reales en una forma sencilla. Aquí te proponemos una forma sencilla para aprender a sumar y restar mediante dos reglas muy fáciles de recordar:

Si se tienen dos números de signos iguales, entonces se suman (entendido como suma en números naturales) y se deja el mismo signo. Ejemplo: 3+5 = 8 esta es una suma común y corriente entre naturales, pero y si fuera -3-5 = -8; observa que igual se obtiene 8 como en la anterior pero esta vez es de signo negativo porque ambos números son negativos y en realidad estamos avanzando hacia la izquierda sobre la recta real.

Si se tienen dos números de signos diferentes, entonces se restan (entendido como resta entre números naturales, el mayor menos el menor) y se deja el signo de la magnitud mayor.

Ejemplo: 5 – 3 = 2 -5 + 3 = -2

Mira estos otros ejemplos:

-7+10=3 que es lo mismo que 10 - 7=3 o

7-10 = -3 que es lo mismo que –10+7 = -3

a) -4-2-5-10= -21 b) 4+2+5+10= 21

En estos ejercicios largos es buena idea agrupar por signos, así:

-4+5-10-20+15-7+9 = ?

-4-10-20-7 = -41 5+15+9=29 Y luego restar: -41+29 = -12

Nótese, que se operó entre los resultados anteriormente obtenidos y se volvió a aplicar la regla. Número de signos diferentes “se restan” y el resultado queda con el signo de la magnitud mayor, en este caso 41.

REGLA DE SIGNOS PARA MULTIPLICACIÓN Y DIVISIÓN

LA DE SIGNOS PARA MULTIPLICAR

+	*	+	=	+
-	*	-	=	+
+	*	-	=	-
-	*	+	=	-

REGLA DE SIGNOS PARA DIVIDIR

+	÷	+	=	+
-	÷	-	=	+
+	÷	-	=	-
-	÷	+	=	-

MULTIPLICACIÓN Y DIVISIÓN DE NÚMEROS REALES

Ejemplos aplicando las reglas de los signos:

Para estas operaciones es obvio que debes conocer las tablas de multiplicación y división, es decir que signos iguales dan positivo y signos diferentes negativo.

Ejemplos: